An MMA Elo Rating System
#Webscraping #Data Visualization #Sports Analytics #Python #MMA
This project uses fight outcomes and opponent quality to construct an Elo-based rating system for mixed martial artists. Using these ratings, I generate tables and visualizations identifying the best current fighters, the greatest fighters of all time, the most competitive matchups, and other insights into MMA performance.
Background
I used to closely follow mixed martial arts fights in organizations like the UFC, WEC, and Strikeforce. But starting around 2020, my interest in the sport began to fade, primarily due to inequitable fighter pay and a product that felt increasingly stale. However, my interest in #dataanalysis has only grown. I have long thought about applying a more rigorous, transparent rating system to MMA, especially since rankings and recent performance often determine who receives opportunities to fight for titles. The current ranking system in the UFC, for instance, is based on UFC-selected media member rankings. Not exactly an unbiased sample of voters. This is when I had the idea to apply an Elo-based rating system to provide a more data-driven and unbiased view of the best mixed martial artists.
Elo ratings
The Elo rating system was originally developed as a way to measure the relative skill of chess players and can be applied to any zero-sum game, including football, board games like Scrabble, and even Pokémon battles. The main idea is that player quality is inferred from their performance against other players, taking opponent quality into account. In each match, a player has an expected score, or probability of winning, and their ELO rating updates based on the match outcome (win, loss, or draw), the expected score, and the maximum possible adjustment per game (K-factor). The K-factor can be adjusted based on player quality or match frequency, but a fairly standard-sized K-factor for games played at high frequency is around 30.
Data Collection/Webscraping
To establish Elo ratings for mixed martial artists, we need to obtain results for each fight (win, lose, draw, no contest, etc.), the opponent, the rankings of each fighter at the time of their bout, and optionally, as we will see, whether the fight was a finish (KO/TKO or submission) or a championship fight. Gathering this data is not a small feat, as, to my knowledge, no database currently exists that houses all this information.
Therefore, to construct this ranking system, I began by scraping event pages, notable alumni lists, or current active rosters from Wikipedia to build a dataset of fighters. The list of MMA organizations (including those now defunct) includes:
- UFC
- Pride
- WEC
- Strikeforce
- PFL
- Bellator
- Invicta
- Rizin
I then build a dataset of fighters and scrape their Wikipedia pages, gathering data on: weight class, gender, and individual bout info such as outcome, opponent, date, and method of victory.1 Overall, I establish a dataset of nearly 45,000 fights across about 3,800 individual fighters.
Elo Ratings
In this section, I outline how the ELO ratings are constructed. If you’d rather skip the math, feel free to move on to the result section and check out the tables and figures.
I calculate the Elo ratings as follows:
Each fighter begins with a baseline Elo rating. The model uses informative priors to assign the baseline rating. Let:
- n = number of profession fights
- W = indicator for having a Wikipedia page
- W = 1 if the fighter has a Wikipedia page
- W = 0 otherwise
If a fighter has more than 10 professional fights, they receive a baseline rating of 1500. If the fighter has fewer than 10 fights but has a Wikipedia page, I take this to mean that the fighter is more notable and may be of higher quality. Their baseline therefore, ranges between 1300 and 1500, scaling linearly depending on the number of fights they’ve competed in. For fighters without a Wikipedia page and less than 10 points I use a baseline from 1100 and 1500 again scaling linearly based on the number of fights completed. This allows ratings to adjust more realistically based on fighters’ skill levels while also preventing fighters from “stat-padding” wins against lower ability fighters (see e.g., Jeremy Horn).
The K-factor governs the sensitivity of the Elo ratings to new information; the higher the K-factor, the more sensitive the ratings are to change. Games that can be played frequently may have lower K-factors, such as 20, where multiple matches can be played in a single day. However, it is common in MMA to average about 2-4 fights per year, so I use a K-factor of 60. I also employ a dynamic K-factor that scales with opponents’ experience. If a fighter faces an opponent with fewer than five fights the update is dampened, otherwise the update uses the full K value. This prevents large ratings jumps from wins over unproven fighters.
For each bout, I then obtain the expected score, or expected probability of Fighter A winning, $E_A$, based on the rating of Fighter A and Fighter B as:
\[E_A = \frac{1}{1 + 10^{(R_B - R_A)/400}}\]where $R_A$ and $R_B$ are the current or baseline ratings of each fighter. I then define $S_A \in {0, 0.5, 1}$ if the result of the fight is a loss, draw, or win for Fighter A, respectively. Unlike most traditional Elo ratings, I also apply a decay function that accounts for inactivity. Decay functions in Elo ratings are used to prevent individuals from protecting a high ranking by remaining inactive. For MMA, the use of a decay function benefits more active fighters and also penalizes fighters who may duck fights (see e.g., Jon Jones vs. Tom Aspinall). However, some delays between fights are due to injuries, scheduling issues, and fight cancellations. Therefore, I implement a very conservative exponential decay function toward a lower bound to account for inactivity. Fighter A’s inactivity decay is defined as:
\[R_{\text{new}} = R_{\min} + (R_{\text{old}} - R_{\min}) \cdot e^{-\ln(2)\cdot \frac{t}{t_{1/2}}}\]where $R_{\text{new}}$ is the fighters updated rating, $R_{\text{old}}$ is the previous rating, $R_{\text{min}}$ is the lower bound, $t$ is the number of days since Fighter A’s last fight, and $t_{1/2}$ is the half life. I set $R_{\text{min}}$ to 1500 where fighters above 1500 are penalized for inactivity, but those below 1500 are not, and $t_{1/2}$ to 1825. The figure below shows the decay in Elo rating due to inactivity with a half-life of 1825 days. This means that after 5 years of inactivity, the fighter’s rating falls halfway between their current rating (1800) and the floor (1500). Again, this is a conservative decay function, meant to penalize fighters for purposeful inactivity with the caveat that inactivity can arise for multiple reasons outside of the mixed martial artists’ control. Therefore, a fighter loses about 100 points for 3 years of inactivity. It is not a substantial drop in their rating, but it does effectively prevent fighters from sitting on their high rating and may more accurately reflect the fighter’s ability over time.
FIGURE 1: Decay Function

Finally, I incorporate two types of bonuses for wins: 1) finishes and 2) championships. Each fighter receives additional points for each victory that ends in a finish. This rewards dominant performances without over-weighting them, as finishes are positively correlated with weight class. Fighters also receive a bonus for winning a championship fight as it signals higher quality opposition, higher stakes, and in many cases involves extra “championship rounds”. I give greater weight to titles won in top-tier promotions (UFC, PRIDE, WEC, Strikeforce, or Bellator) and award a lower bonus to championships in lower-tier promotions. This tiering system prevents those who dominate lower-tier organizations but infrequently face higher-quality competition from inflating their rating (see e.g., Hector Lombard’s multiple Cage FC title defenses and subsequent UFC run).
The updated rating for Fighter A is then:
\[R_{\text{new}} = R_a + K_a \cdot (S_a - E_a) + Bonus_{Finish} + Bonus_{Championship}\]where $R_{\text{new}}$ is Fighter A’s new rating, $R_a$ is Fighter A’s pre-fight rating, $K_a$ is the K-factor, $S_a$ is the score, $E_a$ is the win probability, and $Bonus_{Finish}$ and $Bonus_{Championship}$ are the additional bonuses. As an example, when Georges St. Pierre fought Jake Shields at UFC 129, St. Pierre’s ELO rating was 1855 while Shields held a rating of 1784. Therefore, GSP’s expected score was 0.6, and as it was a championship fight in a high-tier promotion resulting in a unanimous decision win for GSP, he received the championship bonus but not the finish bonus. Using a championship bonus of 6, his new rating would be 1885.
Results
After creating this dataset, there are so many interesting findings to explore. I supply some here, but feel free to ask for specific requests or try things out yourself!
Peak ELO Ratings
I start by creating a list of the peak ELO ratings achieved by any fighter in Table 1; this rating can be used as one proxy for determining the greatest fighters of all time (GOATs), but capturing sustained success is also an important metric (see below for my GOAT analysis). Anderson Silva achieves the highest peak rating in this model by nearly 28 points over Fedor Emelianenko. Both went on historic runs, but Silva holds on to the top spot after his 10 successful defenses in the UFC middleweight division. Islam Makhachev also cracks the top five peak ratings after his dominant performance over Jack Della Maddalena at UFC 322.
I speculate that the rise of champion vs champion fights across weight classes, starting in 2016 when Conor McGregor moved up to fight Eddie Alvarez for the lightweight title, has contributed to some rating inflation. Eleven of the top thirty fighters and four of the top six fighters by peak ELO rating have been involved in one of these bouts. Henderson is the only fighter to have earned the “double champ” status from this list prior to 2016 (doing so in Pride in 2007).
TABLE 1. Peak ELO Ratings
| Rank | Fighter | Peak ELO Rating | Rank | Fighter | Peak ELO Rating |
|---|---|---|---|---|---|
| 1 | Anderson Silva | 2070.43 | 16 | Dan Henderson | 1941.96 |
| 2 | Fedor Emelianenko | 2042.7 | 17 | Wanderlei Silva | 1939.39 |
| 3 | Georges St-Pierre | 2037.04 | 18 | Donald Cerrone | 1938.09 |
| 4 | Daniel Cormier | 2034.26 | 19 | Israel Adesanya | 1937.7 |
| 5 | Islam Makhachev | 2017.27 | 20 | Max Holloway | 1933.87 |
| 6 | Jon Jones | 2013.62 | 21 | Matt Hughes | 1933.1 |
| 7 | Kamaru Usman | 1991.11 | 22 | Robbie Lawler | 1932.32 |
| 8 | Jose Aldo | 1983.68 | 23 | Chuck Liddell | 1923.76 |
| 9 | Charles Oliveira | 1978.09 | 24 | Benson Henderson | 1920.54 |
| 10 | Gegard Mousasi | 1961.38 | 25 | Mirko Filipovic | 1919.59 |
| 11 | Alexander Volkanovski | 1960.24 | 26 | Merab Dvalishvili | 1916.52 |
| 12 | Antonio Rodrigo Nogueira | 1954.05 | 27 | Valentina Shevchenko | 1915.46 |
| 13 | Ryan Bader | 1950.54 | 28 | Dustin Poirier | 1915.24 |
| 14 | Stipe Miocic | 1946.13 | 29 | Khabib Nurmagomedov | 1909.59 |
| 15 | Demetrious Johnson | 1944.45 | 30 | Justin Gaethje | 1906.25 |
This metric also correlates reasonably well with consensus picks for the greatest fighters, which usually include Silva, St. Pierre, Jones, etc. (see, e.g., community rankings on Tapology). One notable fighter who ranks lower in my ELO rating system than in most rankings is Khabib Nurmagomedov. While Khabib tore through the UFC lightweight division, eventually capturing the belt and retiring undefeated, he barely cracks the top 30 list here. In Figure 1, I plot the ELO Ratings over time of Khabib and some of the other consensus greatest fighters. While Khabib’s rating dropped somewhat between 2014 and 2016 due to a layoff from injuries and one bout cancellation (the first of five attempts to schedule the infamous never-to-be fight between Nurmagomedov and Tony Ferguson), Khabib’s rating is mostly stunted due to a string of fights against lesser competition early in his career. In his first sixteen professional fights, he only faced two fighters notable enough to have their own Wikipedia page, twelve of whom never competed in more than five professional fights. These opponents had a combined record of 47-51-1 and excluding the two “notable” fighters, they had a combined record of 7-38. Given that these lower-quality matches make up over half of Khabib’s career fights, his peak rating seems much more reasonable.
FIGURE 2: ELO Trajectories of MMA Greats

Best Current Mixed Martial Artists
Table 2 lists the current best fighters by ELO rating. Note that I only include fighters who have been active in the last two years. Here we see Islam Makhachev at the top of the heap. Makhachev has been on a tremendous string of wins and increased his ELO rating by 161 points after beating perennial favorites Charles Oliveira (9th peak all-time ELO at the time of the fight), Alexander Volkanovski (11th peak all-time ELO), and Dustin Poirier (28th). We will see if he can extend his lead in the rankings by facing current UFC lightweight champion Ilia Topuria (#7), who has been calling for a match with Makhachev. Valentina Shevchenko, Zhang Weili, and Cris Cyborg are also the top three women who enter the list. In the near future, I plan to extend this analysis to WMMA and create current rankings by weight class for both women and men.
TABLE 2. Best Current Fighters by ELO Rating
| Rank | Fighter | ELO Rating | Rank | Fighter | ELO Rating |
|---|---|---|---|---|---|
| 1 | Islam Makhachev | 2017.27 | 16 | Kamaru Usman | 1837.29 |
| 2 | Max Holloway | 1922.47 | 17 | Alexandre Pantoja | 1837.26 |
| 3 | Merab Dvalishvili | 1916.52 | 18 | Dricus du Plessis | 1836.57 |
| 4 | Valentina Shevchenko | 1915.46 | 19 | Cris Cyborg | 1833.03 |
| 5 | Charles Oliveira | 1911.49 | 20 | Khamzat Chimaev | 1832.97 |
| 6 | Justin Gaethje | 1881.59 | 21 | Zhang Weili | 1830.83 |
| 7 | Ilia Topuria | 1881.32 | 22 | Ryan Bader | 1828.57 |
| 8 | Alexander Volkanovski | 1873.67 | 23 | Arman Tsarukyan | 1821.55 |
| 9 | Jiri Prochazka | 1870.78 | 24 | Corey Anderson | 1814.36 |
| 10 | Alex Pereira | 1868.29 | 25 | Movsar Evloev | 1813.95 |
| 11 | Jon Jones | 1858.65 | 26 | Dustin Poirier | 1804.73 |
| 12 | Aljamain Sterling | 1852.83 | 27 | Kyoji Horiguchi | 1803.47 |
| 13 | Magomed Ankalaev | 1850.57 | 28 | Francis Ngannou | 1802.6 |
| 14 | Shavkat Rakhmonov | 1850.38 | 29 | Ciryl Gane | 1802.24 |
| 15 | Alexander Volkov | 1839.23 | 30 | Vadim Nemkov | 1793.86 |
Greatest Fights
I also sum the ELO ratings of fighters and their opponents to create a list of the top fights of all time in Table 3. By Elo rating, the trilogy fight between Daniel Cormier and Stipe Miocic tops the list at numbers 1, 2, and 5 all-time. Cormier is involved in five of the top ten fights on the list, with his 1st fight against Jon Jones and fight against Derrick Lewis coming in at #9 and #10, respectively. Cormier vs Jones 2 does not crack the top 10 as it was ruled a no-contest (omitted from the dataset) after Jones failed a drug test.
TABLE 3. Greatest Fights by ELO Rating
| Rank | Fighter 1 | ELO Rating 1 | Fighter 2 | ELO Rating 2 | Combined ELO Rating |
|---|---|---|---|---|---|
| 1 | Daniel Cormier | 2030.82 | Stipe Miocic | 1868.08 | 3898.9 |
| 2 | Stipe Miocic | 1911.88 | Daniel Cormier | 1978.91 | 3890.78 |
| 3 | Georges St-Pierre | 1993.45 | Jake Shields | 1892.6 | 3886.05 |
| 4 | Anderson Silva | 2042.21 | Chael Sonnen | 1836.61 | 3878.82 |
| 5 | Daniel Cormier | 1970.61 | Stipe Miocic | 1904.49 | 3875.1 |
| 6 | Islam Makhachev | 1913.84 | Alexander Volkanovski | 1946.78 | 3860.62 |
| 7 | Johny Hendricks | 1845.11 | Georges St-Pierre | 2014.62 | 3859.73 |
| 8 | Anderson Silva | 2029.78 | Yushin Okami | 1819.45 | 3849.24 |
| 9 | Daniel Cormier | 1856.03 | Jon Jones | 1988.54 | 3844.57 |
| 10 | Daniel Cormier | 2011.19 | Derrick Lewis | 1821.44 | 3832.63 |
ELO vs Win Rate
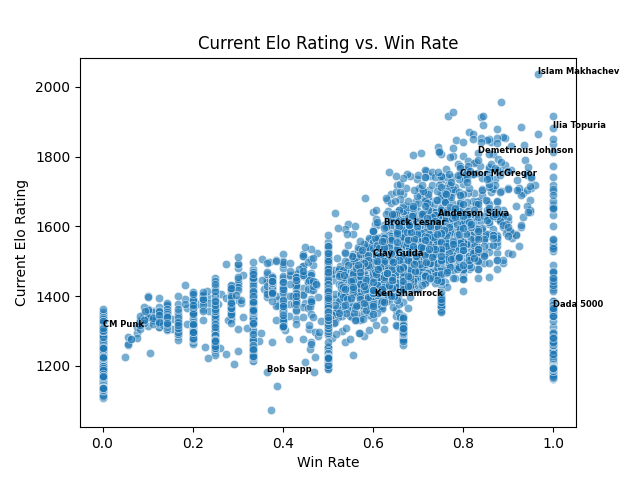
In Figure 2, I plot the current ELO ratings and fighters’ win rate percentages. Overall, we see a positive correlation between win rate and ELO rating. On the bottom left corner of the figure, we see lower-level fighters such as WWE star turned MMA wannabe CM Punk, moving up and to the right, we start to see fighters like Clay Guida, who are “gatekeepers” of their weight classes, high-level fighters that never quite made it to the upper echelon. Beyond that, we see elite-level fighters like Demetrious Johnson and Ilia Topuria (and a bit lower, we have Dada 5000 with his uhh interesting fight with Kimbo Slice).
FIGURE 3: ELO Rating vs Win Rate %
ELO over Time
Figure 4 plots the top 10 ELO ratings over time using a bar chart race. While the first recorded MMA match was in 1980 (Rei Zulu vs. Rickson Gracie), fights were relatively uncommon (five fights in the 1980s) until 1993, when both Pancrase and the UFC held their first events. Therefore, this bar chart begins in 1993, updating the top 10 ELO ratings every month thereafter.
FIGURE 4: ELO Ratings Since 1993

MMA GOAT
The final analysis I will share in this post is a multi-metric assessment attempting to quantify the greatest mixed martial artists of all time. I use four distinct metrics: 1) peak ELO rating, 2) area under the ELO curve (AUEC), 3) strength of schedule (SoS), and 4) quality-adjusted wins (QAW). I then standardize each metric to have a mean of 0 and a standard deviation of 1 and sum them together to create a Legacy Score. The peak ELO rating, as presented in Table 1, is again the highest ELO rating a fighter achieves at the pinnacle of their career. The AUEC captures sustained success by measuring how long and how far above an elite level a fighter stayed over their career. The AUEC is defined as:
\[AUEC = \sum_{i = 1}^{N} max(ELO_{i} - ELO_{threshold}, 0) \times \Delta t\]where $N$ is the number of fights in a fighter’s career, $E_{i}$ is the fighter’s ELO rating before fight $i$, $ELO_{threshold}$ is the cutoff for an elite fighter, which I define as 1600, and $\Delta t_{i}$ is the number of days between fights. Therefore, every day a fighter stays above the elite-level threshold contributes to their score. This measure weighs both peak achievements and sustained success, so a fighter who is moderately successful is comparable to a fighter who reached a higher peak but had a shorter career (e.g., Jim Miller vs. Anthony Pettis).
SoS is simply the mean ELO rating of opponents a fighter faces, i.e.:
\[SoS = \frac{1}{N} \sum_{i=1}^{N} E_{i}^{opp}\]where $N$ is the number of fights in a fighter’s career and $E_{i}^{opp}$ is the pre-fight ELO rating of the opponent for each fight $i$. Using this measure in the legacy score rewards fighters who consistently fight high-level opponents compared to those who pad their records against low-level competition.
The last measure, QAW is defined as:
\[QAW = \sum_{i=1}^{N} \max(E_{i}^{\text{opp}} - E_{\text{baseline}}, 0)\,\mathbb{1}\{\text{win}_{i}\}\]where $E_{i}^{opp}$ is again the opponent’s pre-fight ELO rating, $E_{baseline}$ is the average-level fighter who had a sustained career in MMA (1500), and $\mathbb{1}{\text{win}_{i}}$ is an indicator equal to 1 if the fighter wone fight $i$ and 0 otherwise. This measure rewards those who have won against high-level competition.
The sample of fighters used in this analysis is as follows. First, I only use fights from 1993 or later. This prevents those who fought infrequently in the 1980s from distorting the AUEC metric. Second, I restrict the sample to fighters with at least ten professional bouts and a minimum career length of five years. Any legitimate all-time great comfortably exceeds these thresholds, and the filters help remove short-career or low-activity fighters who would contribute noise rather than information. Importantly, these filters also ensure that z-scores for each metric are calculated relative to a population of reasonably accomplished fighters, which is more appropriate for assessing the greatest mixed martial artists of all time. By focusing on athletes with meaningful careers, the resulting comparisons are more relevant for evaluating long-term excellence.
After standardizing these measures, the Legacy Score is then:
\[Legacy Score = z_{peak ELO} + z_{AUEC} + z_{SoS} + z_{QAW}\]Table 4 lists the top ten fighters by Legacy Score alongside their standardized metrics. Fedor, GSP, Jones, and Silva take the top spots, which is highly consistent with most subjective lists where they are typically ranked in the all-time top five. Perhaps most surprising in this list is Lyoto Machida. While he certainly had a great career, challenging for UFC titles in two weight classes and capturing the belt at light heavyweight, he also has the lowest peak ELO rating among this group. Machida’s Legacy Score is mainly bolstered by his tough strength of schedule and strong quality-adjusted wins; throughout his career, he faced unusually elite opposition, including 20 bouts against current or former UFC, PRIDE, Bellator, or Strikeforce champions.
Two main patterns emerge from this analysis. First, heavyweight fighters tend to dominate the rankings. This appears to stem from structural features of the division. There are simply fewer athletes large enough to compete at heavyweight, which means the number of elite heavyweights at any time is small. Because organizations heavily promote the division, established heavyweights often receive more opportunities, remain in the spotlight longer, and accumulate long careers. These factors likely inflate AUEC scores.
Second, on the other end of the size distribution, fighters in lower weight classes tend to underperform in this ranking system. A prominent example is Demetrious Johnson, the long-time 125-pound UFC champion, typically considered a top-ten fighter of all time, who comes in at only #32. He is also the only fighter in the top 50 from the bantamweight or flyweight divisions (excluding Frankie Edgar’s brief late-career run at bantamweight). Lower-weight fighters seem disadvantaged by lower SoS and QAW scores. This likely reflects MMA’s history: these divisions were introduced much later than heavier ones. The WEC was the first major organization to feature weight classes below 155 lbs (beginning in 2001), the UFC did not incorporate them until acquiring the WEC in 2010, and the UFC flyweight division was created only in 2012. As a result, these fighters had fewer years to accumulate AUEC and fewer highly-rated opponents available to boost SoS and QAW. This is evident in the table from José Aldo’s SoS and QAW scores, despite facing some of the most accomplished opponents in featherweight and bantamweight history.
TABLE 4. MMA Greatest of All Time List
| Rank | Fighter | z-Peak Elo | z-AUEC | z-SoS | z-QAW | Score |
|---|---|---|---|---|---|---|
| 1 | Fedor Emelianenko | 4.24 | 10 | 2.16 | 2.15 | 18.55 |
| 2 | Georges St-Pierre | 4.19 | 7.23 | 2.97 | 2.8 | 17.19 |
| 3 | Jon Jones | 3.95 | 7.91 | 2.43 | 2.41 | 16.7 |
| 4 | Anderson Silva | 4.53 | 7.69 | 2.18 | 2.21 | 16.6 |
| 5 | Jose Aldo | 3.65 | 7.05 | 2 | 1.7 | 14.4 |
| 6 | Antonio Rodrigo Nogueira | 3.35 | 6.01 | 2.44 | 2.33 | 14.13 |
| 7 | Dan Henderson | 3.22 | 5.21 | 2.92 | 2.56 | 13.92 |
| 8 | Daniel Cormier | 4.16 | 4.44 | 2.78 | 2.11 | 13.49 |
| 9 | Lyoto Machida | 2.72 | 5.17 | 2.9 | 2.41 | 13.19 |
| 10 | Josh Barnett | 2.75 | 6.12 | 2.13 | 1.92 | 12.92 |
Overall, the Legacy Score performs well in identifying the sport’s consensus all-time greats. A natural next step would be to reweight the score by weight class to address structural differences across divisions, which I leave for future work.
Code
If you’d like to explore this dataset more, you can find the data and code here.